ゲーム理論の無線通信への応用

　無線通信の利用により，電波が届く範囲であれば有線での配線が難しい場所でも通信を成り立たせることが可能です．これは，電波が様々な方向に放射される同報性があるためです．一方で，同一周波数帯で同時に異なる複数の無線通信を行おうとすると，受信局において単純には同一チャネル干渉が生じます．この同一チャネル干渉は，複数の無線通信の間の相互作用と捉えることができます．
　このような相互作用—特に複数の意思決定主体の間に存在する相互作用—がある状況における意思決定を扱う数学理論として，ゲーム理論（Game Theory）が知られています．ゲーム理論は経済学で発展してきた理論であり，端的に言えばゲームと呼ばれるある種の最適化問題を扱う数学理論と言えます．ゲームの中で最もシンプルな戦略形2人ゲームとは，次式のような問題設定のことを指します．
　\begin{cases} \max_{a_1} u_1(a_1, a_2) \\ \max_{a_2} u_2(a_1, a_2) \end{cases}
片方の式のみであれば単純な最適化問題であり，上の最適化問題は a_2 を固定した場合に関数 u_1 が最大となる変数 a_1 及びその場合の関数 u_1 の値を求めるという問題に過ぎません．ただ，2つの最適化問題が同時に存在するため，下の問題に上の問題の解が影響を与え，更に上の問題の解が下の問題の解にも影響を与えます．これが戦略形ゲームで定式化できる相互作用です．
　無線通信システムでは，各無線局のスループットや遅延といった通信品質は，自局の送信電力や使用周波数といったパラメータのみならず，干渉により他局のパラメータ設定にも依存します．詳細は省きますが，通信組のインデックスの集合を \mathcal{N} = \{1,2,\dots,N\} と表記し，通信組 i の送信電力を p_i ，通信路容量を u_i というように表せば，
　\displaystyle u_i(p_i,p_{-i}) = \log_2 \left( 1+\frac{G_{ii}p_i}{\displaystyle\sum_{ j \in \mathcal{N} \setminus \{i\}}G_{ij}p_j + N_i} \right)
と，先の最適化問題のような形となることが分かります．従って，電力制御やチャネル割当といった無線リソースを分散的に制御する際に，ゲーム理論を応用することが可能です．これまでに，ポテンシャルゲーム，進化ゲーム，少数派ゲームといった様々なゲームに対する知見を用い，干渉制御のための送信制御手法を提案しています．

戦略形ゲームにおけるナッシュ均衡

3d_ua

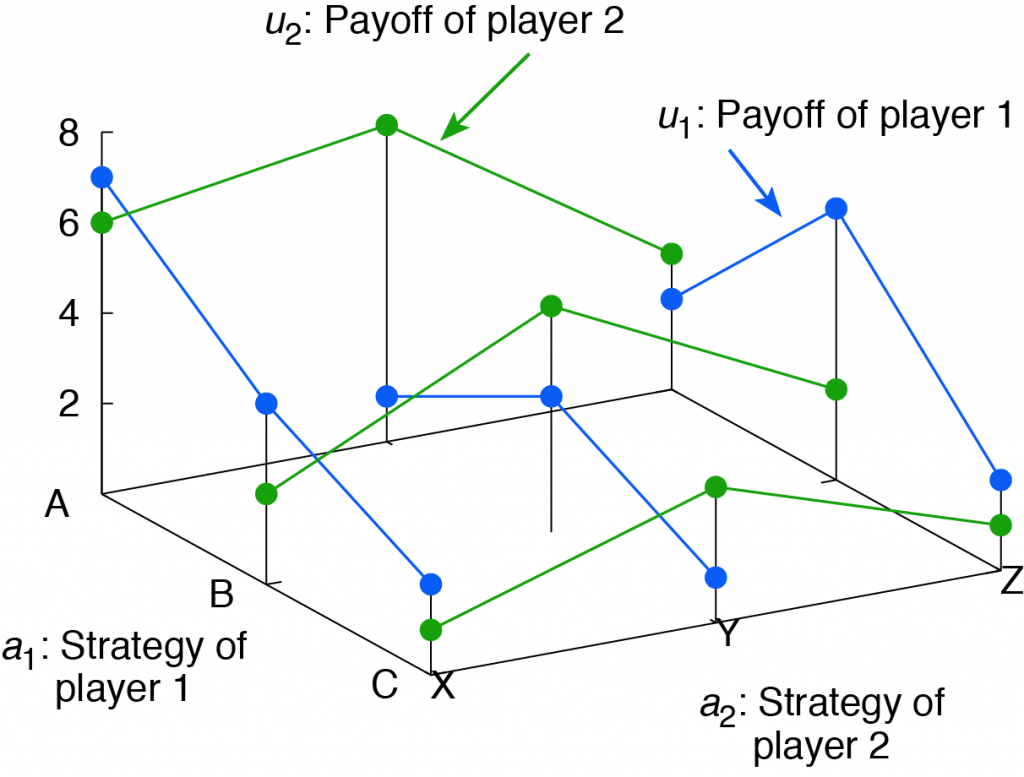
　戦略形ゲームの解概念は，ナッシュ均衡と呼ばれるものです．ナッシュ均衡は，各プレーヤは自分の戦略のみを変更することでは利得関数をそれ以上上げられない戦略の組合せとして定義されます．式で表すと次の条件を満たす (a_1^\star,a_2^\star) がナッシュ均衡です．
　\begin{cases} u_1(a_1^\star,a_2^\star) = \displaystyle\max_{a_1}\; u_1(a_1,a_2^\star) \\ u_2(a_1^\star,a_2^\star) = \displaystyle\max_{a_2}\; u_2(a_1^\star,a_2) \end{cases}
　例として，図により定義されるゲームのナッシュ均衡を説明します．この図では，各プレーヤの戦略の変更により利得関数を変化できる方向のみ線で繋いでおり，u_1 はプレーヤ1が a_1 を変化させることで意図的に変化できるため a_1 方向に線を結んでいますが，a_2 方向には結んでいない．
　図におけるナッシュ均衡は，結論から述べると，(a_1,a_2)=(\text{B}, \text{Y})という1点のみです．これは u_1 を結ぶ線と u_2 を結ぶ線の両方が最大となる点であり，そのような点は他には存在しないためです．この点ではいずれのプレーヤも自分のみが戦略を変更する限りにおいては利得を上げることが出来ません．
　まず点 (a_1,a_2)=(\text{A}, \text{X}) を考えます．この点は，ナッシュ均衡ではありません．これは，プレーヤ2は戦略を a_2=\text{X} から a_2=\text{Y} に変化させることで自分の利得 u_2 を増加させられるためです．変化させた点 (a_1,a_2)=(\text{A}, \text{Y}) もナッシュ均衡ではありません．今度はプレーヤ1が戦略をa_1=\text{A}からa_1=\text{B}に変化させることで利得u_1を増加させられるためです．最終的に，さらに変化させた点(a_1,a_2)=(\text{B}, \text{Y})が先に述べた通りナッシュ均衡です．
　ゲーム理論に関する簡単な導入としては [山本2012] を，頻繁に用いられるゲームのクラスであるポテンシャルゲームに関しては [Yamamoto2015] を参照ください．